Entri Populer

Minggu, 03 April 2016

tugas rangkuman fisika (Jum'at 15 April 2016)

TEORI KINETIK GAS

Di pertengahan abad ke-19, ilmuwan mengembangkan suatu teori baru untuk menggantikan teori kalorik. Teori ini bedasarkan pada anggapan bahwa zat disusun oleh partikel-partikel sangat kecil yang selalu bergerak. Bunyi teori Kinetik adalah sebagai berikut:
Dalam benda yang panas, partikel-partikel bergerak lebih cepat dan karena itu memiliki energi yang lebih besar daripada partikel-partikel dalam benda yang lebih dingin.
Teori Kinetik (atau teori kinetik pada gas) berupaya menjelaskan sifat-sifat makroscopik gas, seperti tekanan, suhu, atau volume, dengan memperhatikan komposisi molekular mereka dan gerakannya. Intinya, teori ini menyatakan bahwa tekanan tidaklah disebabkan oleh denyut-denyut statis di antara molekul-molekul, seperti yang diduga Isaac Newton, melainkan disebabkan oleh tumbukan antarmolekul yang bergerak pada kecepatan yang berbeda-beda. Teori Kinetik dikenal pula sebagai Teori Kinetik-Molekular atau Teori Tumbukan atau Teori Kinetik pada Gas.


Teori untuk gas ideal memiliki asumsi-asumsi berikut ini:
  • Gas terdiri dari partikel-partikel sangat kecil, dengan massa tidak nol.
  • Banyaknya molekul sangatlah banyak, sehingga perlakuan statistika dapat diterapkan.
  • Molekul-molekul ini bergerak secara konstan sekaligus acak. Partikel-partike yang bergerak sangat cepat itu secara konstan bertumbukan dengan dinding-dinding wadah.
  • Tumbukan-tumbukan partikel gas terhadap dinding wadah bersifat lenting (elastis) sempurna.
  • Interaksi antarmolekul dapat diabaikan (negligible). Mereka tidak mengeluarkan gaya satu sama lain, kecuali saat tumbukan terjadi.
  • Keseluruhan volume molekul-molekul gas individual dapat diabaikan bila dibandingkan dengan volume wadah. Ini setara dengan menyatakan bahwa jarak rata-rata antarpartikel gas cukuplah besar bila dibandingkan dengan ukuran mereka.
  • Molekul-molekul berbentuk bulat (bola) sempurna, dan bersifat lentur (elastic).
  • Energi kinetik rata-rata partikel-partikel gas hanya bergantung kepada suhu sistem.
  • Efek-efek relativistik dapat diabaikan.
  • Efek-efek Mekanika kuantum dapat diabaikan. Artinya bahwa jarak antarpartikel lebih besar daripada panjang gelombang panas de Broglie dan molekul-molekul dapat diperlakukan sebagai objek klasik.
  • Waktu selama terjadinya tumbukan molekul dengan dinding wadah dapat diabaikan karena berbanding lurus terhadap waktu selang antartumbukan.
  • Persamaan-persamaan gerak molekul berbanding terbalik terhadap waktu.
Lebih banyak pengembangan menenangkan asumsi-asumsi ini dan didasarkan pada Persamaan Boltzmann. Ini dapat secara akurat menjelaskan sifat-sifat gas padat, sebab mereka menyertakan volume molekul. Asumsi-asumsi penting adalah ketiadaan efek-efek quantum, kekacauan molekular dan gradien kecil di dalam sifat-sifat banyaknya. Perluasan terhadap orde yang lebih tinggi dalam kepadatan dikenal sebagai perluasan virial. Karya definitif adalah buku tulisan Chapman dan Enskog, tetepi terdapat pengembangan yang lebih modern dan terdapat pendekatan alternatif yang dikembangkan oleh Grad, didasarkan pada perluasan momentum. Di dalam batasan lainnya, untuk gas yang diperjarang, gradien-gradien di dalam sifat-sifat besarnya tidaklah kecil bila dibandingkan dengan lintasan-lintasan bebas rata-ratanya. Ini dikenal sebagai rezim Knudsen regime dan perluasan-perluasannya dapat dinyatakan dengan Bilangan Knudsen.
Teori Kinetik juga telah diperluas untuk memasukkan tumbukan tidak lenting di dalam materi butiran oleh Jenkins dan kawan-kawan.

Tekanan

Tekanan dapat dijelaskan oleh teori kinetik sebagai kemunculan dari gaya yang dihasilkan oleh molekul-molekul gas yang menabrak dinding wadah. Misalkan suatu gas denagn N molekul, masing-masing bermassa m, terisolasi di dalam wadah yang mirip kubus bervolume V. Ketika sebuah molekul gas menumbuk dinding wadah yang tegak lurus terhadap sumbu koordinat x dan memantul dengan arah berlawanan pada laju yang sama (suatu tumbukan lenting), maka momentum yang dilepaskan oleh partikel dan diraih oleh dinding adalah:
\Delta p_x = p_i - p_f = 2 m v_x\,
di mana vx adalah komponen-x dari kecepatan awal partikel.
Partikel ini memberi tumbukan kepada dinding sekali setiap 2l/vx satuan waktu (di mana l adalah panjang wadah). Kendati partikel menumbuk sebuah dinding sekali setiap 1l/vx satuan waktu, hanya perubahan momentum pada dinding yang dianggap, sehingga partikel menghasilkan perubahan momentum pada dinding tertentu sekali setiap 2l/vx satuan waktu.
\Delta t = \frac{2l}{v_x}
gaya yang dimunculkan partikel ini adalah:
F = \frac{\Delta p}{\Delta t} = \frac{2 m v_x}{\frac{2l}{v_x}} = \frac{m v_x^2}{l}
Keseluruhan gaya yang menumbuk dinding adalah:
F = \frac{m\sum_j v_{jx}^2}{l}
di mana hasil jumlahnya adalah semua molekul gas di dalam wadah.
Besaran kecepatan untuk tiap-tiap partikel mengikuti persamaan ini:
v^2 = v_x^2 + v_y^2 + v_z^2
Kini perhatikan gaya keseluruhan yang menumbuk keenam-enam dinding, dengan menambahkan sumbangan dari tiap-tiap arah, kita punya:
\mbox{Total Force} = 2 \cdot \frac{m}{l}(\sum_j v_{jx}^2 + \sum_j v_{jy}^2 + \sum_j v_{jz}^2) = 2 \cdot \frac{m}{l} \sum_j (v_{jx}^2 + v_{jy}^2 + v_{jz}^2) = 2 \cdot \frac{m \sum_j v_{j}^2}{l}
di mana faktor dua muncul sejak saat ini, dengan memperhatikan kedua-dua dinding menurut arah yang diberikan.
Misalkan ada sejumlah besar partikel yang bergerak cukup acak, gaay pada tiap-tiap dinding akan hampir sama dan kini perhatikanlah gaya pada satu dinding saja, kita punya:
F = \frac{1}{6} \left(2 \cdot \frac{m \sum_j v_{j}^2}{l}\right) = \frac{m \sum_j v_{j}^2}{3l}
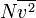Kuantitas \sum_j v_{j}^2 dapat dituliskan sebagai {N} \overline{v^2}, di mana garis atas menunjukkan rata-rata, pada kasus ini rata-rata semua partikel. Kuantitas ini juga dinyatakan dengan v_{rms}^2 di mana v_{rms} dalah akar kuadrat rata-rata kecepatan semua partikel.
Jadi, gaya dapat dituliskan sebagai:
F = \frac{Nmv_{rms}^2}{3l}
Tekanan, yakni gaya per satuan luas, dari gas dapat dituliskan sebagai:
P = \frac{F}{A} = \frac{Nmv_{rms}^2}{3Al}
di mana A adalah luas dinding sasaran gaya.
Jadi, karena luas bagian yang berseberangan dikali dengan panjang sama dengan volume, kita punya pernyataan berikut untuk tekanan
P = {Nmv_{rms}^2 \over 3V}
di mana V adalah volume. Maka kita punya
PV = {Nmv_{rms}^2 \over 3}
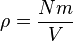Karena Nm adalah masa keseluruhan gas, maka kepadatan adalah massa dibagi oleh volume \rho = {Nm \over V} .
Maka tekanan adalah
P = {2 \over 3} \frac{\rho\ v_{rms}^2}{2}
Hasil ini menarik dan penting, sebab ia menghubungkan tekanan, sifat makroskopik, terhadap energi kinetik translasional rata-rata per molekul {1 \over 2} mv_{rms}^2 yakni suatu sifat mikroskopik. Ketahuilah bahwa hasil kali tekanan dan volume adalah sepertiga dari keseluruhan energi kinetik.

Suhu dan energi kinetik

Dari hukum gas ideal
PV=Nk_BT(1)
dimana B adalah konstanta Boltzmann dan T adalah suhu absolut. Dan dari rumus diatas, dihasilkan Gagal memparse (kesalahan sintaks): PV={Nmv_{rms}^2\overset 3} Derivat:
Nk_BT=\frac{Nmv_{rms}^2}{3}
T=\frac{mv_{rms}^2}{3k_B}(2)
yang menuju ke fungsi energi kinetik dari sebuah molekul
mv_{rms}^2=3k_BT
Energi kinetik dari sistem adalah N kali lipat dari molekul K=\frac{Nmv_{rms}^2}{2}
Suhunya menjadi
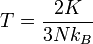T=\frac{2K}{3Nk_B}(3)
Persamaan 3 ini adalah salah satu hasil penting dari teori kinetik
Dari persamaan 1 dan 3 didapat:
PV=\frac{2K}{3}(4)
Dengan demikian, hasil dari tekanan dan volume tiap mol sebanding dengan rerata energi kinetik molekuler. Persamaan 1 dan 4 disebut dengan hasil klasik, yang juga dapat diturunkan dari mekanika statistik[1].
Karena 3N adalah derajat kebebasan (DK) dalam sebuah sistem gas monoatomik dengan N partikel, energi kinetik tiap DK adalah:
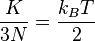\frac{K}{3 N}=\frac{k_B T}{2}(5)
Dalam energi kinetik tiap DK, konstanta kesetaraan suhu adalah setengah dari konstanta Boltzmann. Hasil ini berhubungan dengan teorema ekuipartisi. Seperti yang dijelaskan pada artikel kapasitas bahang, gas diatomik seharusnya mempunyai 7 derajat kebebasan, tetapi gas yang lebih ringan berlaku sebagai gas yang hanya mempunyai 5. Dengan demikian, energi kinetik tiap kelvin (gas ideal monoatomik) adalah:
  • Tiap mole: 12.47 J
  • Tiap molekul: 20.7 yJ = 129 μeV
Pada STP (273,15 K , 1 atm), didapat:
  • Tiap mole: 3406 J
  • Tiap molekul: 5.65 zJ = 35.2 meV

Banyaknya tumbukan dengan dinding

Jumlah tumbukan atom dengan dinding wadah tiap satuan luar tiap satuan waktu dapat diketahui. Asumsikan pada gas ideal, derivasi dari [2] menghasilkan persamaan untuk jumlah seluruh tumbukan tiap satuan waktu tiap satuan luas:
A=\frac{N\cdot v_{avg}}{4V}=\frac{\rho}{4}\sqrt{\frac{8kT}{\pi m}}\frac{1}{m}.

Laju RMS molekul

Dari persamaan energi kinetik dapat ditunjukkan bahwa:
v_{rms}^2=\frac{3RT}{\mbox{massa mol}}
dengan v pada m/s, T pada kelvin, dan R adalah konstanta gas. Massa molar diberikan sebagai kg/mol. Kelajuan paling mungkin adalah 81.6% dari kelajuan RMS, dan rerata kelajuannya 92.1% (distribusi kelajuan Maxwell-Boltzmann).

Banyaknya tumbukan dengan dinding

One can calculate the number of atomic or molecular collisions with a wall of a container per unit area per unit time.
Assuming an ideal gas, a derivation[3] results in an equation for total number of collisions per unit time per area:
A = \frac{1}{4}\frac{N}{V} v_{avg} = \frac{\rho}{4} \sqrt{\frac{8 k T}{\pi m}} \frac{1}{m}. \,

Laju RMS molekul

From the kinetic energy formula it can be shown that
(v_{rms})^2 = \frac{3RT}{\mbox{massa molar}}
dengan v dalam m/s, T dalam kelvin, dan R adalah konstanta gas. Satuan dari massa molar adalah kg/mol.


 contoh soal :





Soal No. 1
16 gram gas Oksigen (M = 32 gr/mol) berada pada tekanan 1 atm dan suhu 27oC. Tentukan volume gas jika:
a) diberikan nilai R = 8,314 J/mol.K
b) diberikan nilai R = 8314 J/kmol.K


Pembahasan
a) untuk nilai R = 8,314 J/mol.K
Data :
R = 8,314 J/mol.K
T = 27oC = 300 K
n = 16 gr : 32 gr/mol = 0,5 mol
P = 1 atm = 105 N/m2



b) untuk nilai R = 8314 J/kmol.K

Data :
R = 8314 J/kmol.K
T = 27oC = 300 K
n = 16 gr : 32 gr/mol = 0,5 mol
P = 1 atm = 105 N/m2



Soal No. 2
Gas bermassa 4 kg bersuhu 27oC berada dalam tabung yang berlubang.



Jika tabung dipanasi hingga suhu 127oC, dan pemuaian tabung diabaikan tentukan:
a) massa gas yang tersisa di tabung
b) massa gas yang keluar dari tabung
c) perbandingan massa gas yang keluar dari tabung dengan massa awal gas
d) perbandingan massa gas yang tersisa dalam tabung dengan massa awal gas
e) perbandingan massa gas yang keluar dari tabung dengan massa gas yang tersisa dalam tabung

Pembahasan
Data :
Massa gas awal m1 = 4 kg
Massa gas tersisa m2
Massa gas yang keluar dari tabung Δ m = m2 − m1

a) massa gas yang tersisa di tabung



b) massa gas yang keluar dari tabung



c) perbandingan massa gas yang keluar dari tabung dengan massa awal gas



d) perbandingan massa gas yang tersisa dalam tabung dengan massa awal gas



e) perbandingan massa gas yang keluar dari tabung dengan massa gas yang tersisa dalam tabung



Soal No. 3
A dan B dihubungkan dengan suatu pipa sempit. Suhu gas di A adalah 127oC dan jumlah partikel gas di A tiga kali jumlah partikel di B.



Jika volume B seperempat volume A, tentukan suhu gas di B!

Pembahasan
Data :
TA = 127oC = 400 K
NA : NB = 2 : 1
VA : VB = 4 : 1



Soal No. 4
Gas dalam ruang tertutup memiliki suhu sebesar T Kelvin energi kinetik rata-rata Ek = 1200 joule dan laju efektif V = 20 m/s.



Jika suhu gas dinaikkan hingga menjadi 2T tentukan:
a) perbandingan energi kinetik rata-rata gas kondisi akhir terhadap kondisi awalnya
b) energi kinetik rata-rata akhir
c) perbandingan laju efektif gas kondisi akhir terhadap kondisi awalnya
d) laju efektif akhir

Pembahasan
a) perbandingan energi kinetik rata-rata gas kondisi akhir terhadap kondisi awalnya



b) energi kinetik rata-rata akhir



c) perbandingan laju efektif gas kondisi akhir terhadap kondisi awalnya



d) laju efektif akhir



Soal No. 5
Sebuah ruang tertutup berisi gas ideal dengan suhu T dan kecepatan partikel gas di dalamnya v. Jika suhu gas itu dinaikkan menjadi 2T maka kecepatan partikel gas tersebut menjadi …
A. √2 v
B. 12 v
C. 2 v
D. 4 v
E. v2
(Dari soal Ebtanas 1990)

Pembahasan
Data dari soal adalah:
T1 = T
T2 = 2T
V1 = ν
v2 =.....

Kecepatan gas untuk dua suhu yang berbeda



Sehingga diperoleh



Soal No. 6
Didalam sebuah ruangan tertutup terdapat gas dengan suhu 27oC. Apabila gas dipanaskan sampai energi kinetiknya menjadi 5 kali energi semula, maka gas itu harus dipanaskan sampai suhu …
A. 100oC
B. 135oC
C. 1.200oC
D. 1.227oC
E. 1.500oC
(Soal Ebtanas 1992)

Pembahasan
Data diambil dari soal
T1 = 27°C = 27 + 273 = 300 K
Ek2 = 5 Ek1
T2 = .....
Energi kinetik gas untuk dua suhu yang berbeda



Sehingga diperoleh



Dalam Celcius adalah = 1500 − 273 = 1227°C
Soal No. 7
Di dalam ruang tertutup suhu suatu gas 27°C, tekanan 1 atm dan volume 0,5 liter. Jika suhu gas dinaikkan menjadi 327°C dan tekanan menjadi 2 atm, maka volume gas menjadi....
A. 1 liter
B. 0,5 liter
C. 0,25 liter
D. 0,125 liter
E. 0,0625 liter

Pembahasan
Data soal:
T1 = 27°C = 300 K
P1 = 1 atm
V1 = 0,5 liter

T2 = 327°C = 600 K
P2 = 2 atm
V2 = ..........

P1 V1               P2 V2
_______ = _______
T1                 T2

(1)(0,5)       (2) V2
_______ = _______
300                600

V2 = 0,5 liter

Soal No. 8
Suatu gas ideal mula-mula menempati ruang yang volumenya V dan tekanan P. Jika suhu gas menjadi 5/4 T dan volumenya menjadi 3/4 V, maka tekanannya menjadi….
A. 3/4 P
B. 4/3 P
C. 3/2 P
D. 5/3 P
E. 2 P
(UN 2010 PO4)

Pembahasan



Soal No. 9
Gas dengan volume V berada di dalam ruang tertutup bertekanan P dan bersuhu T. Bila gas mengembang secara isobarik sehingga volumenya menjadi 1/2 kali volume mula-mula, maka perbandingan suhu gas mula-mula dan akhir adalah....(UN Fisika 2014)
A. 1 : 1
B. 1 : 2
C. 1 : 3
D. 2 : 1
E. 3 : 2

Pembahasan
Data soal:
P1 = P → 1
T1 = T → 1
Isobaris artinya tekanannya sama P1 = P2 → 1
Volumenya menjadi 1/2 kali volume mula-mula artinya:
V2 = 1
V1 = 2
T1 : T2 =....



Soal No. 10
Suatu gas ideal mula-mula menempati ruangan yang volumenya V dan suhu T dan tekanan P.
   Tabung I        Tabung II


Jika gas dipanaskan kondisinya seperti pada tabung 2, maka volume gas menjadi....(UN Fisika 2014)
A. 1/2 V
B. 8/9 V
C. 9/8 V
D. 2/3 V
E. 3/2 V

Pembahasan
Data soal:
Tekanan menjadi 4/3 mula-mula:
P1 = 3
P2 = 4
Suhu menjadi 3/2 mula-mula:
T1 = 2
T2 = 3
V2 = ..... V1

Diposting oleh di

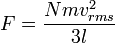
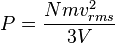
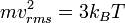
Tidak ada komentar:

Posting Komentar

Langganan: Posting Komentar (Atom)